⑤匹配库数据扫描
在 DBSCAN 算法中构成集群的形式化依赖于一些定义 。 首先 ， 点 p 的邻域 N(p) 是距离 p 小于或等于 p 的所有点的集合 。 如果点的邻域包含至少最少数量的点 ， 则点被标记为核心点 。 核心点 q 的邻域中的任何点 p 都被称为从核心点直接密度可达 。 如果存在一系列点 p1 ， 则任何点 p 都是从核心点 q 密度可达的. . , pn, p1 = q, pn = p 使得 pi+1 可直接从 pi 密度可达 。 密度可达条件的对称变体是密度连通的 ， 两个点 p 和 q 是密度连通的 ， 如果它们存在一个点 o ， 那么这两个点都是密度可达的 。 一个簇被定义为所有密度连接的点 ， 从集群内的任何点密度可达的点也包括在内 ， 而无法到达的点被标记为异常值 。
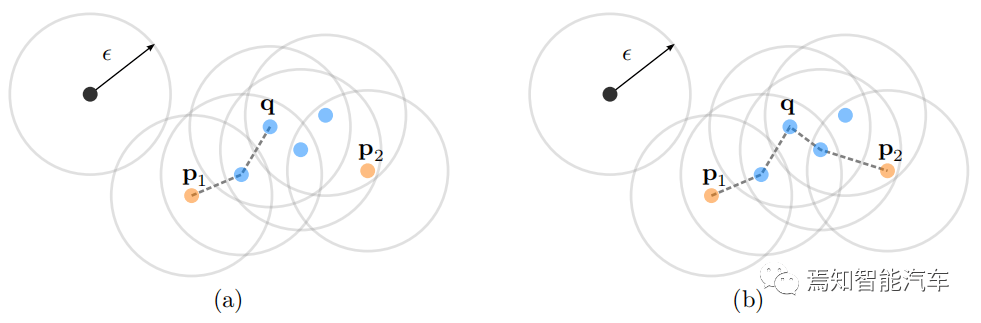
下图以图形方式显示了不同的可达性定义：

文章图片

最小样本参数等于 4 点的 DBSCAN 可达性说明：上图中蓝色圆圈是核心点 ， 因为它们的邻域至少包含最少数量的点 。 图(a)中点 p1 是从 q 密度可达的 ， 图(b) 中 p1 和 p2 通过核心点 q 彼此密度连接 ， 黑点被标记为异常值 。
DBSCAN 聚类呈现出有利的特征 ， 因为它几乎不需要对数据集进行假设 。 不必指定簇的数量 ， 可以找到任意形状的簇 。 此外 ， 异常值是固有地检测到的 。 该算法的一个缺点是它无法对密度不同的数据集进行聚类 。
为了在跟踪点上应用 DBSCAN 聚类算法 ， 数据被组织成一个聚类矩阵 C ， 其中 Nf,k 是在时间 k 跟踪的特征点的数量 ， d是包含在聚类中的维数 。 预计源自单个物体的轨迹将表现出类似的时间行为 ， 同时以欧几里德距离紧密间隔 。 鉴于此 ， 聚类矩阵的每一行都是一个形式为的表达式 。 其中pWi表示世界参考系中跟踪点 pi的平均值, vi是该点在过去有限数量的时间步长内的平均速度 。 常数 c 是衡量速度分量贡献的加权因子 。 该实现有利于速度维度的比例为 3:1 ， 即 c = 3 。 在聚类过程中 ， 普通欧几里得距离用作相异度量 。 由如上方程的特征向量产生的集群预测会包含表象中的相似空间和时间行为的点 。
一个标签 ， 表明 DBSCAN 程序产生的集群和异常值的组成 ， 离群点被立即丢弃 。 为了从视觉系统获得最终的测量结果 ， 内部集群对其平均速度进行了阈值处理 。
每个输出集群都应包含源自同一移动对象的点 。 在数学方面 ， 集群测量可以写成一组点 ， 即 ， 其中 Nc 是特定点的数量簇 。 可以在任何给定的时间步长提取大量集群 ， 建议从视觉系统中提取的测量值的一组表示 ， 即 ， 其中Ncam,k是数字在时间 k 的集群测量 。 请注意 ， 如上方程的聚类特征向量的形式导致世界坐标系下参考帧的输出测量 。
特别是 ， 使用了特征跟踪器的金字塔式实现 ， 其输出被视为特征的“测量” 。 随后使用卡尔曼滤波器的测量更新方程处理该测量 ， 视差是通过查询密集深度图像获得的 ， 生成的特征轨迹为具有足够纹理的图像区域并提供了相应的速度信息 ， 而这些速度的术语是一种场景流 ， 它是具有深度信息的二维光流的扩展 。

文章图片