理想的几何形状意味着独特的对极线对是平行的 ， 并且共轭对不会做垂直偏移 ， 这使得能够在立体图像对的适用行上简单地执行对应搜索 。 具有这些理想特性的立体图像称为校正 。 立体校正的过程涉及通过图像处理程序对两个图像进行变换 ， 校正还需要了解两个相机之间的物理排列 ， 即外在参数 。 与内在相机校准一样 ， 用于计算立体视觉设置的外在参数的标准方法可以参照当前一些文献获得 。
首先关键的问题是估计两个摄像头传感器参考系之间的刚体变换 ， 获取描述这种变换的外在参数的最简单方法是通过物理测量几何排列 。 然而 ， 由于难以准确地确定各个传感器的实际起源 ， 这样的过程可能会导致较差的估计 。 改进的估计应该来自自动校准方法 ， 其中传感器需要测量相同的目标 。 然后可以将校准转化为参数优化问题 ， 以求解外部参数 。 优化过程可通过将摄像头结合雷达探测目标的参数融合校准过程进行 。
假设相机对摄像头参考帧CRF中的点 pC进行了测量 。 同样在摄像头参考帧中的测量值由给 出 。 此外 ， 结合使用雷达的相位单脉冲 ， 雷达参考帧RRF中相同对象的测量结果表示如下：
（7）
其中 α 是与视轴的逆时针角度 ， 即方位角 。 符号用于描述雷达参考帧中的测量深度信息 。 而摄像头参考帧中相同测量的坐标由下式给出：

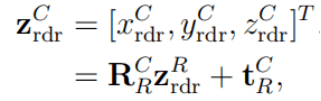
文章图片

（8）
其中 RCR、tCR分别表示是雷达参考帧相对于摄像头参考帧的旋转矩阵及平移坐标向量 。 方程 (8) 描述的三维旋转和平移遵循约定 ， 其中旋转被分解为围绕摄像头参考帧的 z、y 和 x 轴的旋转序列 ， 相应的旋转角分别由角度ψ、θ和φ给出 。 三维变换的欧拉参数化完全由这些角度和平移向量 tCR= [tx, ty, tz]T的元素定义 。 因此 ， 外部参数的确定简化为 ψ、θ、φ、tx、ty和 tz的求解 。
上面的讨论假设影响相应测量值和形成的内在参数是已知的 。 无需调整现有的用于立体相机内部和外部参数的校准方法 。 因此 ， 演示将继续假设立体视觉相机经过校准以产生校正图像 。 对于雷达 ， 天线基线可以被视为一个内在参数 。 如果基线指定不正确 ， 优化产生的外部雷达到相机参数将是不正确的 。 因为当不作为测量基线时 ， 而是作为额外的自由参数包括在校准程序中进行估计 。
目标参数测量、匹配及提取
对于摄像头和雷达融合的校准过程需要一个对两个传感器子系统都可见的校准目标 。 为此 ， 通过在面向传感器的三个反射面上应用棋盘格纸图案来增强简单的角反射器 。 由此产生的校准目标既具有高反射性（高 RCS） ， 又包含尖角 ， 可以在立体图像对中找到精确的对应关系 。

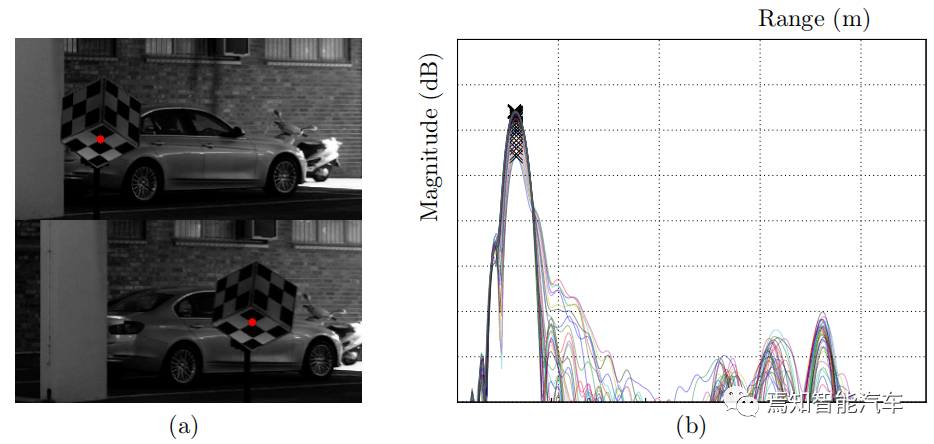
文章图片

图(a)立体图像对中的引导角选择
图(b)雷达范围频谱中的引导局部峰值
确保参数估计所考虑的任何测量都源自校准目标是至关重要的 。 出于这个原因 ， 原始传感器数据被手动标记 。 标记雷达数据就像识别距离谱中与校准目标相对应的峰值一样简单 。 只需要对目标范围的粗略估计 ， 选择加上角反射器极高的雷达截面 。 提取的数据包括到目标的距离以及两个接收器的信号相位 ， 这些相位用于随后的角度计算 。 为了提高精度 ， 需要进行24 次扫描 ， 并取得平均距离和角度构成单个雷达校准样本 ， 其结果可以描述在各个脉冲范围谱中发现的局部峰值 。