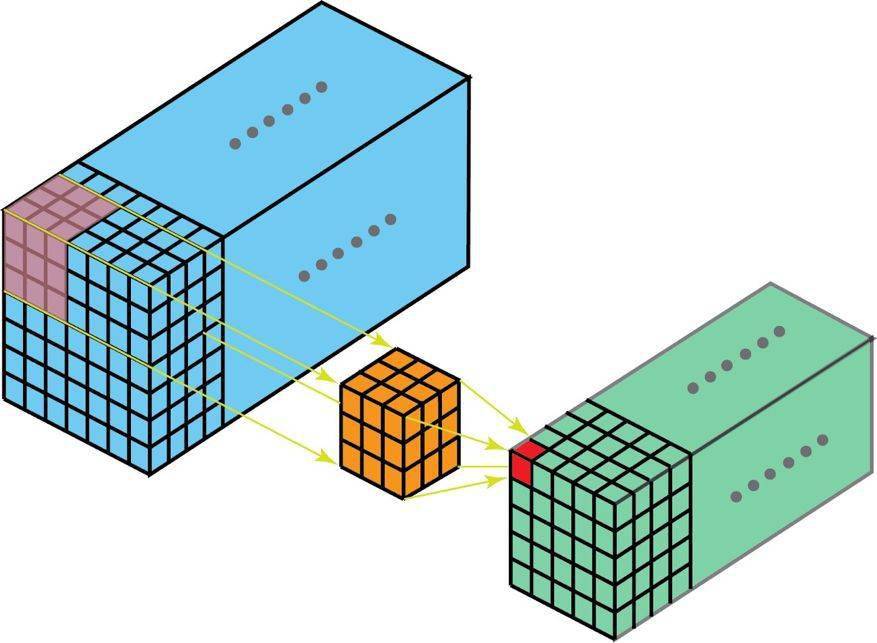
很自然 ， 3D 卷积确实存在 。 这是 2D 卷积的泛化 。 下面就是 3D 卷积 ， 其过滤器深度小于输入层深度（核大小<通道大小） 。 因此 ， 3D 过滤器可以在所有三个方向（图像的高度、宽度、通道）上移动 。 在每个位置 ， 逐元素的乘法和加法都会提供一个数值 。 因为过滤器是滑过一个 3D 空间 ， 所以输出数值也按 3D 空间排布 。 也就是说输出是一个 3D 数据 。

文章图片

在 3D 卷积中 ， 3D 过滤器可以在所有三个方向（图像的高度、宽度、通道）上移动 。 在每个位置 ， 逐元素的乘法和加法都会提供一个数值 。 因为过滤器是滑过一个 3D 空间 ， 所以输出数值也按 3D 空间排布 。 也就是说输出是一个 3D 数据 。
与 2D 卷积（编码了 2D 域中目标的空间关系）类似 ， 3D 卷积可以描述 3D 空间中目标的空间关系 。 对某些应用（比如生物医学影像中的 3D 分割/重构）而言 ， 这样的 3D 关系很重要 ， 比如在 CT 和 MRI 中 ， 血管之类的目标会在 3D 空间中蜿蜒曲折 。
转置卷积（去卷积）
对于很多网络架构的很多应用而言 ， 我们往往需要进行与普通卷积方向相反的转换 ， 即我们希望执行上采样 。 例子包括生成高分辨率图像以及将低维特征图映射到高维空间 ， 比如在自动编码器或形义分割中 。 （在后者的例子中 ， 形义分割首先会提取编码器中的特征图 ， 然后在解码器中恢复原来的图像大小 ， 使其可以分类原始图像中的每个像素 。 ）
实现上采样的传统方法是应用插值方案或人工创建规则 。 而神经网络等现代架构则倾向于让网络自己自动学习合适的变换 ， 无需人类干预 。 为了做到这一点 ， 我们可以使用转置卷积 。
转置卷积在文献中也被称为去卷积或 fractionally strided convolution 。 但是 ， 需要指出「去卷积（deconvolution）」这个名称并不是很合适 ， 因为转置卷积并非信号/图像处理领域定义的那种真正的去卷积 。 从技术上讲 ， 信号处理中的去卷积是卷积运算的逆运算 。 但这里却不是这种运算 。 因此 ， 某些作者强烈反对将转置卷积称为去卷积 。 人们称之为去卷积主要是因为这样说很简单 。 后面我们会介绍为什么将这种运算称为转置卷积更自然且更合适 。
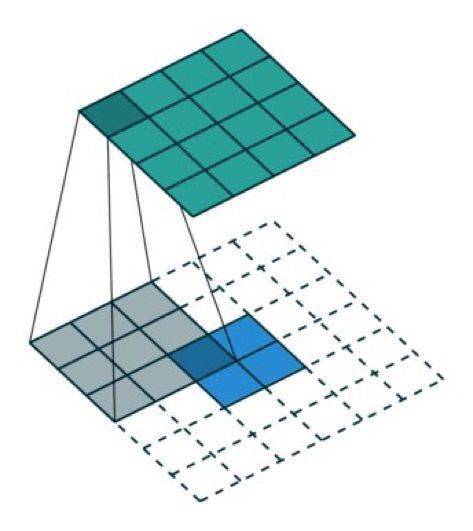
我们一直都可以使用直接的卷积实现转置卷积 。 对于下图的例子 ， 我们在一个 2×2 的输入（周围加了 2×2 的单位步长的零填充）上应用一个 3×3 核的转置卷积 。 上采样输出的大小是 4×4 。

文章图片

将 2×2 的输入上采样成 4×4 的输出
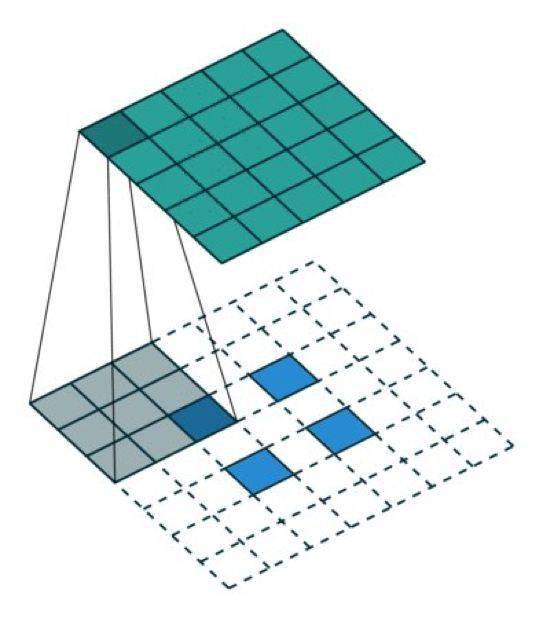
有趣的是 ， 通过应用各种填充和步长 ， 我们可以将同样的 2×2 输入图像映射到不同的图像尺寸 。 下面 ， 转置卷积被用在了同一张 2×2 输入上（输入之间插入了一个零 ， 并且周围加了 2×2 的单位步长的零填充） ， 所得输出的大小是 5×5 。

文章图片

将 2×2 的输入上采样成 5×5 的输出
观察上述例子中的转置卷积能帮助我们构建起一些直观认识 。 但为了泛化其应用 ， 了解其可以如何通过计算机的矩阵乘法实现是有益的 。 从这一点上我们也可以看到为何「转置卷积」才是合适的名称 。
在卷积中 ， 我们定义 C 为卷积核 ， Large 为输入图像 ， Small 为输出图像 。 经过卷积（矩阵乘法）后 ， 我们将大图像下采样为小图像 。 这种矩阵乘法的卷积的实现遵照：C x Large = Small 。