我们都知道卷积的重要性 ， 但你知道深度学习领域的卷积究竟是什么 ， 又有多少种类吗？研究学者 Kunlun Bai 发布了一篇介绍深度学习的卷积文章 ， 用浅显易懂的方式介绍了深度学习领域的各种卷积及其优势 。
>>>>
如果你听说过深度学习中不同种类的卷积（比如 2D / 3D / 1x1 /转置/扩张（Atrous）/空间可分/深度可分/平展/分组/混洗分组卷积） ， 并且搞不清楚它们究竟是什么意思 ， 那么这篇文章就是为你写的 ， 能帮你理解它们实际的工作方式 。
在这篇文章中 ， 我会归纳总结深度学习中常用的几种卷积 ， 并会试图用一种每个人都能理解的方式解释它们 。 除了本文之外 ， 还有一些关于这一主题的好文章 ， 请参看原文 。
希望本文能帮助你构建起对卷积的直观认知 ， 并成为你研究或学习的有用参考 。
本文目录
1.卷积与互相关
2.深度学习中的卷积（单通道版本 ， 多通道版本）
3.3D 卷积
4.1×1 卷积
5.卷积算术
6.转置卷积（去卷积、棋盘效应）
7.扩张卷积
8.可分卷积（空间可分卷积 ， 深度可分卷积）
9.平展卷积
10.分组卷积
11.混洗分组卷积
12.逐点分组卷积
卷积与互相关
在信号处理、图像处理和其它工程/科学领域 ， 卷积都是一种使用广泛的技术 。 在深度学习领域 ， 卷积神经网络（CNN）这种模型架构就得名于这种技术 。 但是 ， 深度学习领域的卷积本质上是信号/图像处理领域内的互相关（cross-correlation） 。 这两种操作之间存在细微的差别 。
无需太过深入细节 ， 我们就能看到这个差别 。 在信号/图像处理领域 ， 卷积的定义是：
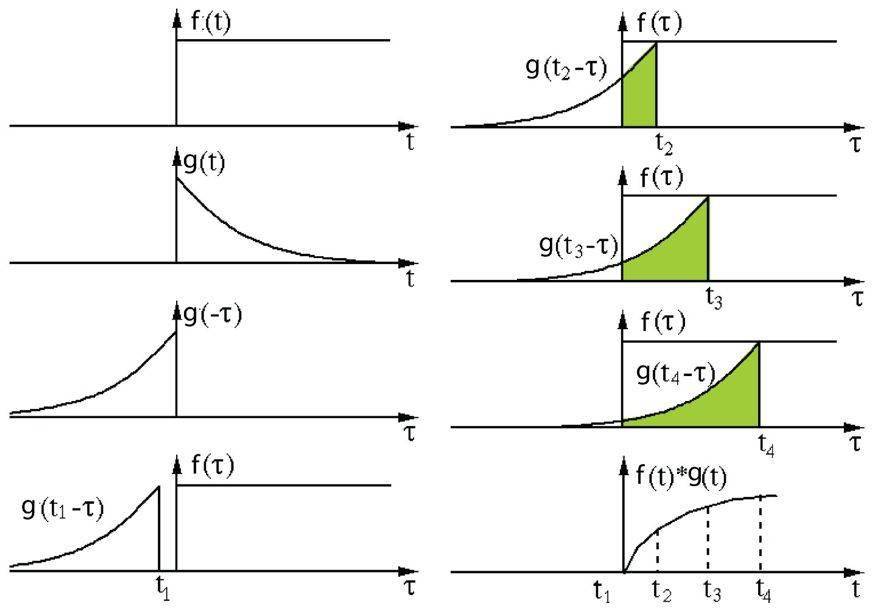
其定义是两个函数中一个函数经过反转和位移后再相乘得到的积的积分 。 下面的可视化展示了这一思想：

文章图片

信号处理中的卷积 。 过滤器 g 经过反转 ， 然后再沿水平轴滑动 。 在每一个位置 ， 我们都计算 f 和反转后的 g 之间相交区域的面积 。 这个相交区域的面积就是特定位置出的卷积值 。
这里 ， 函数 g 是过滤器 。 它被反转后再沿水平轴滑动 。 在每一个位置 ， 我们都计算 f 和反转后的 g 之间相交区域的面积 。 这个相交区域的面积就是特定位置出的卷积值 。
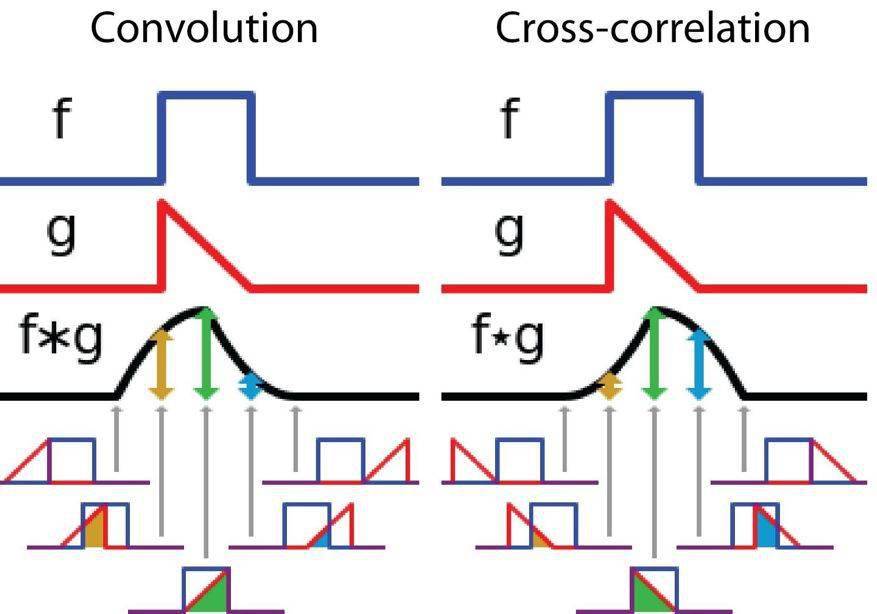
另一方面 ， 互相关是两个函数之间的滑动点积或滑动内积 。 互相关中的过滤器不经过反转 ， 而是直接滑过函数 f 。 f 与 g 之间的交叉区域即是互相关 。 下图展示了卷积与互相关之间的差异 。

文章图片

信号处理中卷积与互相关之间的差异
在深度学习中 ， 卷积中的过滤器不经过反转 。 严格来说 ， 这是互相关 。 我们本质上是执行逐元素乘法和加法 。 但在深度学习中 ， 直接将其称之为卷积更加方便 。 这没什么问题 ， 因为过滤器的权重是在训练阶段学习到的 。 如果上面例子中的反转函数 g 是正确的函数 ， 那么经过训练后 ， 学习得到的过滤器看起来就会像是反转后的函数 g 。 因此 ， 在训练之前 ， 没必要像在真正的卷积中那样首先反转过滤器 。
3D 卷积
在上一节的解释中 ， 我们看到我们实际上是对一个 3D 体积执行卷积 。 但通常而言 ， 我们仍在深度学习中称之为 2D 卷积 。 这是在 3D 体积数据上的 2D 卷积 。 过滤器深度与输入层深度一样 。 这个 3D 过滤器仅沿两个方向移动（图像的高和宽） 。 这种操作的输出是一张 2D 图像（仅有一个通道） 。