Sobel 核可分为一个 3x1 和一个 1x3 核
在卷积中 ， 3×3 核直接与图像卷积 。 在空间可分卷积中 ， 3×1 核首先与图像卷积 ， 然后再应用 1×3 核 。 这样 ， 执行同样的操作时仅需 6 个参数 ， 而不是 9 个 。
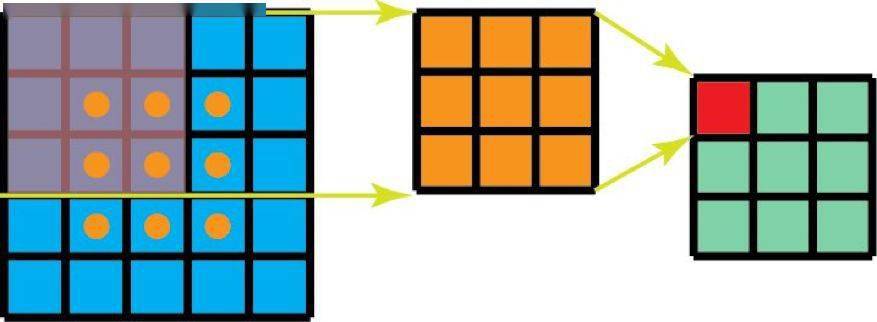
此外 ， 使用空间可分卷积时所需的矩阵乘法也更少 。 给一个具体的例子 ， 5×5 图像与 3×3 核的卷积（步幅=1 ， 填充=0）要求在 3 个位置水平地扫描核（还有 3 个垂直的位置） 。 总共就是 9 个位置 ， 表示为下图中的点 。 在每个位置 ， 会应用 9 次逐元素乘法 。 总共就是 9×9=81 次乘法 。

文章图片

具有 1 个通道的标准卷积
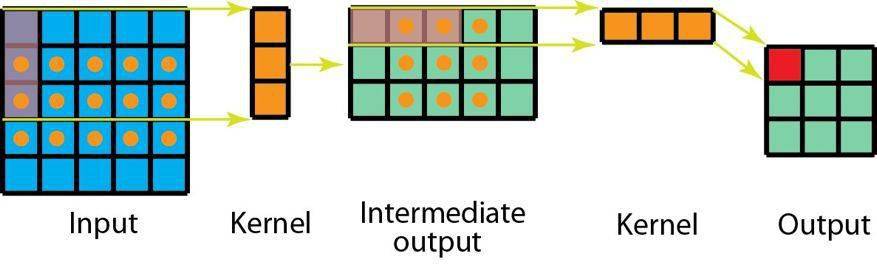
另一方面 ， 对于空间可分卷积 ， 我们首先在 5×5 的图像上应用一个 3×1 的过滤器 。 我们可以在水平 5 个位置和垂直 3 个位置扫描这样的核 。 总共就是 5×3=15 个位置 ， 表示为下图中的点 。 在每个位置 ， 会应用 3 次逐元素乘法 。 总共就是 15×3=45 次乘法 。 现在我们得到了一个 3×5 的矩阵 。 这个矩阵再与一个 1×3 核卷积 ， 即在水平 3 个位置和垂直 3 个位置扫描这个矩阵 。 对于这 9 个位置中的每一个 ， 应用 3 次逐元素乘法 。 这一步需要 9×3=27 次乘法 。 因此 ， 总体而言 ， 空间可分卷积需要 45+27=72 次乘法 ， 少于普通卷积 。

文章图片

具有 1 个通道的空间可分卷积
我们稍微推广一下上面的例子 。 假设我们现在将卷积应用于一张 N×N 的图像上 ， 卷积核为 m×m ， 步幅为 1 ， 填充为 0 。 传统卷积需要 (N-2) x (N-2) x m x m 次乘法 ， 空间可分卷积需要 N x (N-2) x m + (N-2) x (N-2) x m = (2N-2) x (N-2) x m 次乘法 。 空间可分卷积与标准卷积的计算成本比为：

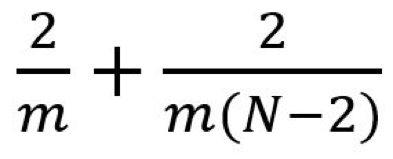
文章图片

因为图像尺寸 N 远大于过滤器大小（N>>m） ， 所以这个比就变成了 2/m 。 也就是说 ， 在这种渐进情况（N>>m）下 ， 当过滤器大小为 3×3 时 ， 空间可分卷积的计算成本是标准卷积的 2/3 。 过滤器大小为 5×5 时这一数值是 2/5；过滤器大小为 7×7 时则为 2/7 。
尽管空间可分卷积能节省成本 ， 但深度学习却很少使用它 。 一大主要原因是并非所有的核都能分成两个更小的核 。 如果我们用空间可分卷积替代所有的传统卷积 ， 那么我们就限制了自己在训练过程中搜索所有可能的核 。 这样得到的训练结果可能是次优的 。
2、深度可分卷积
现在来看深度可分卷积 ， 这在深度学习领域要常用得多（比如 MobileNet 和 Xception） 。 深度可分卷积包含两个步骤：深度卷积核 1×1 卷积 。
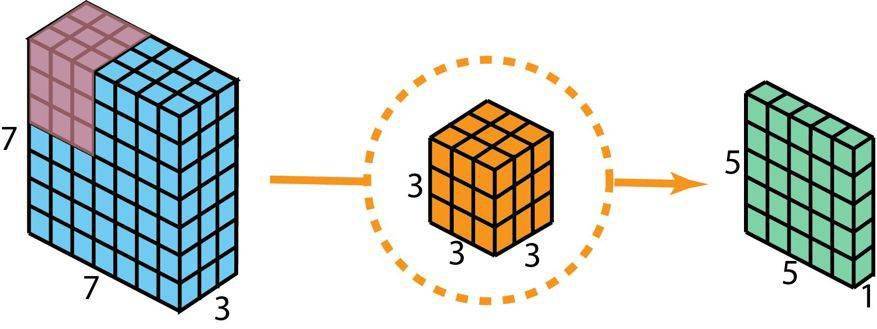
在描述这些步骤之前 ， 有必要回顾一下我们之前介绍的 2D 卷积核 1×1 卷积 。 首先快速回顾标准的 2D 卷积 。 举一个具体例子 ， 假设输入层的大小是 7×7×3（高×宽×通道） ， 而过滤器的大小是 3×3×3 。 经过与一个过滤器的 2D 卷积之后 ， 输出层的大小是 5×5×1（仅有一个通道） 。

文章图片

用于创建仅有 1 层的输出的标准 2D 卷积 ， 使用 1 个过滤器
一般来说 ， 两个神经网络层之间会应用多个过滤器 。 假设我们这里有 128 个过滤器 。 在应用了这 128 个 2D 卷积之后 ， 我们有 128 个 5×5×1 的输出映射图（map） 。 然后我们将这些映射图堆叠成大小为 5×5×128 的单层 。 通过这种操作 ， 我们可将输入层（7×7×3）转换成输出层（5×5×128） 。 空间维度（即高度和宽度）会变小 ， 而深度会增大 。