文章图片

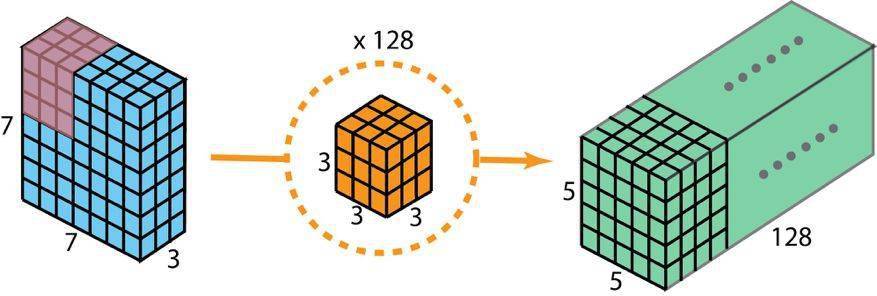
用于创建有 128 层的输出的标准 2D 卷积 ， 要使用 128 个过滤器
现在使用深度可分卷积 ， 看看我们如何实现同样的变换 。
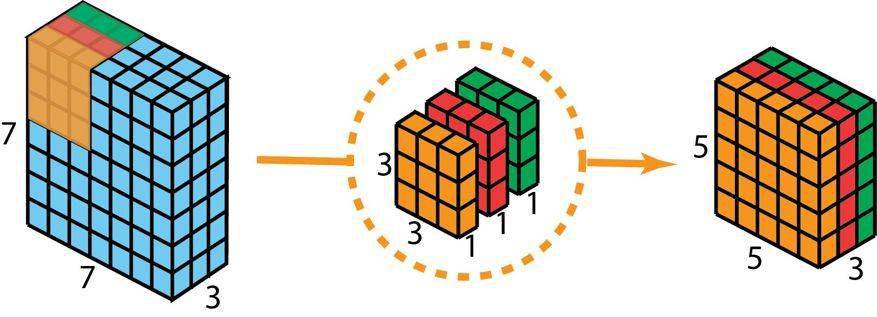
首先 ， 我们将深度卷积应用于输入层 。 但我们不使用 2D 卷积中大小为 3×3×3 的单个过滤器 ， 而是分开使用 3 个核 。 每个过滤器的大小为 3×3×1 。 每个核与输入层的一个通道卷积（仅一个通道 ， 而非所有通道！） 。 每个这样的卷积都能提供大小为 5×5×1 的映射图 。 然后我们将这些映射图堆叠在一起 ， 创建一个 5×5×3 的图像 。 经过这个操作之后 ， 我们得到大小为 5×5×3 的输出 。 现在我们可以降低空间维度了 ， 但深度还是和之前一样 。

文章图片

深度可分卷积——第一步：我们不使用 2D 卷积中大小为 3×3×3 的单个过滤器 ， 而是分开使用 3 个核 。 每个过滤器的大小为 3×3×1 。 每个核与输入层的一个通道卷积（仅一个通道 ， 而非所有通道！） 。 每个这样的卷积都能提供大小为 5×5×1 的映射图 。 然后我们将这些映射图堆叠在一起 ， 创建一个 5×5×3 的图像 。 经过这个操作之后 ， 我们得到大小为 5×5×3 的输出 。
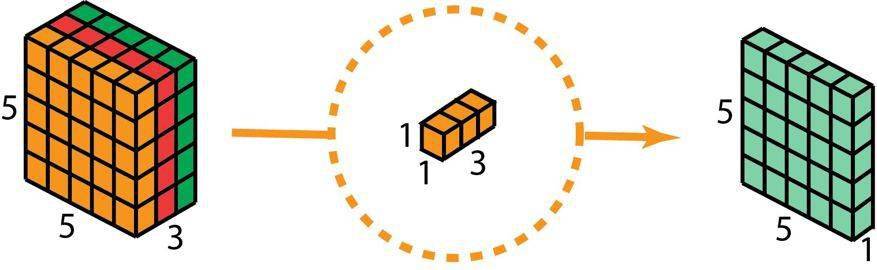
在深度可分卷积的第二步 ， 为了扩展深度 ， 我们应用一个核大小为 1×1×3 的 1×1 卷积 。 将 5×5×3 的输入图像与每个 1×1×3 的核卷积 ， 可得到大小为 5×5×1 的映射图 。

文章图片

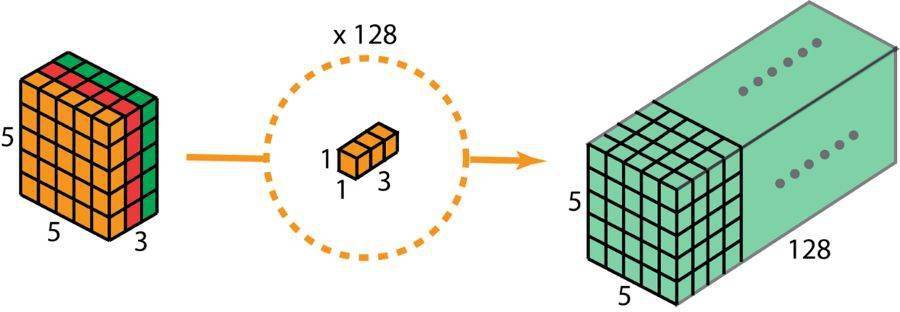
因此 ， 在应用了 128 个 1×1 卷积之后 ， 我们得到大小为 5×5×128 的层 。

文章图片

深度可分卷积——第二步：应用多个 1×1 卷积来修改深度 。
通过这两个步骤 ， 深度可分卷积也会将输入层（7×7×3）变换到输出层（5×5×128） 。
下图展示了深度可分卷积的整个过程 。
深度可分卷积的整个过程
所以 ， 深度可分卷积有何优势呢？效率！相比于 2D 卷积 ， 深度可分卷积所需的操作要少得多 。
回忆一下我们的 2D 卷积例子的计算成本 。 有 128 个 3×3×3 个核移动了 5×5 次 ， 也就是 128 x 3 x 3 x 3 x 5 x 5 = 86400 次乘法 。
可分卷积又如何呢？在第一个深度卷积步骤 ， 有 3 个 3×3×1 核移动 5×5 次 ， 也就是 3x3x3x1x5x5 = 675 次乘法 。 在 1×1 卷积的第二步 ， 有 128 个 1×1×3 核移动 5×5 次 ， 即 128 x 1 x 1 x 3 x 5 x 5 = 9600 次乘法 。 因此 ， 深度可分卷积共有 675 + 9600 = 10275 次乘法 。 这样的成本大概仅有 2D 卷积的 12%！
所以 ， 对于任意尺寸的图像 ， 如果我们应用深度可分卷积 ， 我们可以节省多少时间？让我们泛化以上例子 。 现在 ， 对于大小为 H×W×D 的输入图像 ， 如果使用 Nc 个大小为 h×h×D 的核执行 2D 卷积（步幅为 1 ， 填充为 0 ， 其中 h 是偶数） 。 为了将输入层（H×W×D）变换到输出层（(H-h+1)x (W-h+1) x Nc） ， 所需的总乘法次数为：
Nc x h x h x D x (H-h+1) x (W-h+1)
另一方面 ， 对于同样的变换 ， 深度可分卷积所需的乘法次数为：
D x h x h x 1 x (H-h+1) x (W-h+1) + Nc x 1 x 1 x D x (H-h+1) x (W-h+1) = (h x h + Nc) x D x (H-h+1) x (W-h+1)
则深度可分卷积与 2D 卷积所需的乘法次数比为：

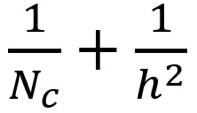
文章图片

现代大多数架构的输出层通常都有很多通道 ， 可达数百甚至上千 。 对于这样的层（Nc >> h） ， 则上式可约简为 1 / h2 。 基于此 ， 如果使用 3×3 过滤器 ， 则 2D 卷积所需的乘法次数是深度可分卷积的 9 倍 。 如果使用 5×5 过滤器 ， 则 2D 卷积所需的乘法次数是深度可分卷积的 25 倍 。