二值化层（Binarization Layer）

• 用于对连续值特征进行划分 。
• 结合逻辑层可实现特征端到端离散化 。

逻辑层（Logical Layer）

• 用于自动学习规则表征 。
• 每个逻辑层由一个合取层和一个析取层构成 。
• 两层逻辑层即可表示合取范式和析取范式 。

线性层（Linear Layer）

• 用于输出分类结果 。
• 可以更好地拟合数据的线性部分.
• 权重可用于衡量规则重要度 。

跳连接（Skip Connection）

• 用于自动跳过不必要的层 。

【鱼和熊掌不可兼得？清华团队提出高准确率的可解释分类模型】
文章图片

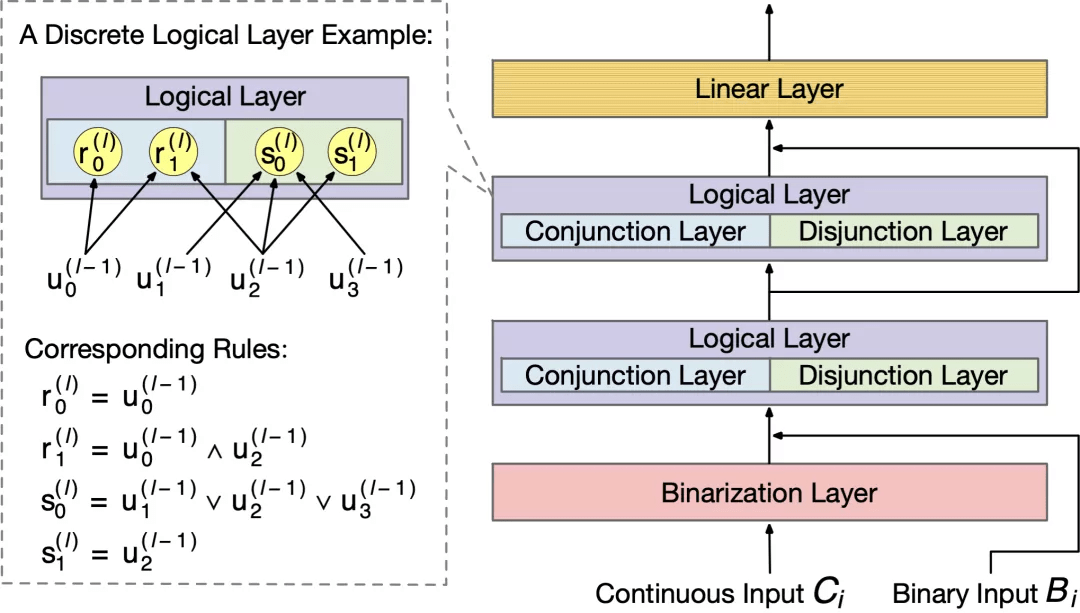
图 2：规则表征学习器举例 。 虚线框中展示了一个离散逻辑层及其对应的规则 。
逻辑层
逻辑层（Logical Layer）使用逻辑规则自动学习数据表征 。 为了实现这一点 ， 逻辑层被设计为同时具有离散版本和连续版本 。 二者共用参数 ， 但离散版本用于训练、测试和解释 ， 而连续版本仅用于训练 。
离散逻辑层
逻辑层中的每个节点都代表了一个逻辑运算 ， 包括合取和析取 ， 而层与层之间边的连接则指明了运算有哪些变量参与 。 离散逻辑层节点对应的逻辑运算如下 ， 其中

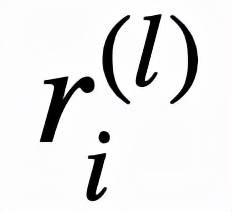
文章图片

和
分别为合取层和析取层中的节点 ，

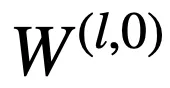
文章图片

和

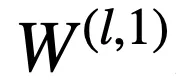
文章图片

则是邻接矩阵 。 图 2 虚线框中展示了一个离散逻辑层的具体例子 。

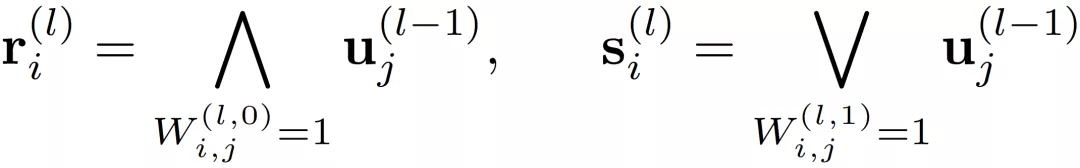
文章图片

通过学习边的连接 ， 逻辑层便可以灵活地表示有着合取或析取范式形式的离散分类规则 。 然而问题在于 ， 虽然离散的逻辑层可解释性好 ， 但自身不可导 ， 难以训练 ， 这也是为什么还需要一个对应的连续版本的逻辑层 。
连续逻辑层
连续逻辑层必须是可导的 ， 并且当二值化连续逻辑层的参数时 ， 可以直接得到它相对应的离散逻辑层 。 为此需要：

• 将 0/1 邻接矩阵替换为 [0, 1] 之间的实数权重矩阵
• 用逻辑激活函数替换逻辑运算

传统的逻辑激活函数（Payani and Fekri, 2019）如下 ， 其中

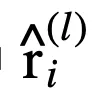
文章图片

和

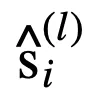
文章图片

分别为连续合取层和连续析取层中的节点 。

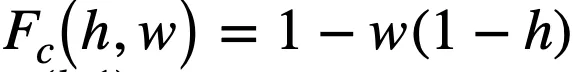
文章图片

而

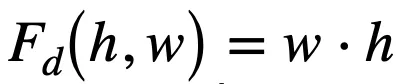
文章图片

， 二者通过

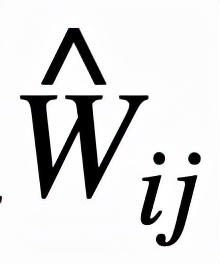
文章图片

的大小来决定

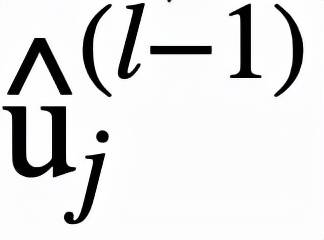
文章图片

对最终结果的影响的大小 。
如果