=0 ， 则 对最终结果没有影响 。 文章图片 虽然这两个逻辑激活函数能够较好地用可导的实数运算模拟逻辑运算 ， 但其存在严重的梯度消失问题 ， 无法处...

=0 ， 则
对最终结果没有影响 。

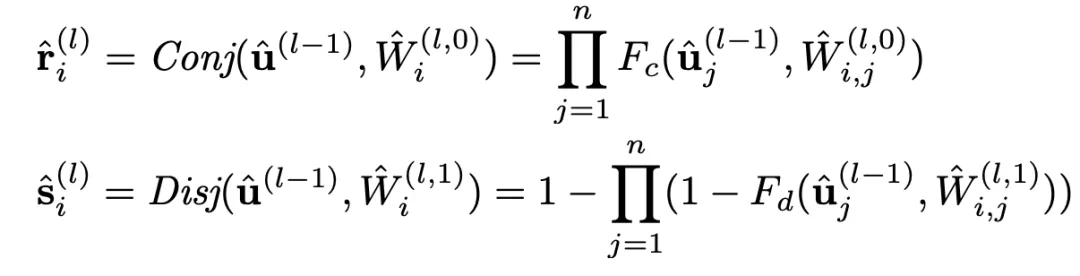
文章图片

虽然这两个逻辑激活函数能够较好地用可导的实数运算模拟逻辑运算 ， 但其存在严重的梯度消失问题 ， 无法处理特征数较多的情况 ， 可扩展性较差 。 分析逻辑激活函数

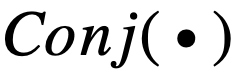
文章图片

和

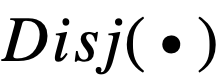
文章图片

以及相应的导数可以发现 ， 使用连乘来模拟逻辑运算是导致梯度消失的主要原因 。
以

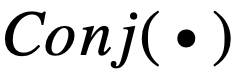
文章图片

为例 ， 其对应导数如下：

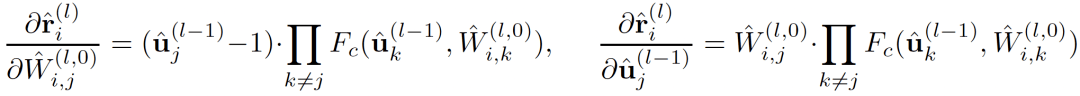
文章图片

由于

文章图片

， 则当相乘的

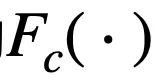
文章图片

数量较多时（一般指特征数较多或节点数较多） ， 导数结果都会趋向于 0 ， 即出现了梯度消失的问题 。
逻辑激活函数改进
传统逻辑激活函数因为使用连乘模拟逻辑运算 ， 因而在处理较多特征时会产生梯度消失的问题 ， 严重损害了模型的可扩展性 。 一个直接的改进思路是使用对数函数将连乘转化为连加 。 然而对数函数使得激活函数无法保持逻辑运算的特性 。 因而需要一个映射函数

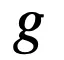
文章图片

， 该映射函数至少需要满足以下三个条件：
条件 (i) 和(ii)用于保持逻辑激活函数的范围和趋势 ， 而条件 (iii) 要求

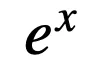
文章图片

是

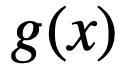
文章图片

的高阶无穷小 ， 主要用于减缓当

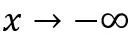
文章图片

时其趋向于 0 的速度 。
取

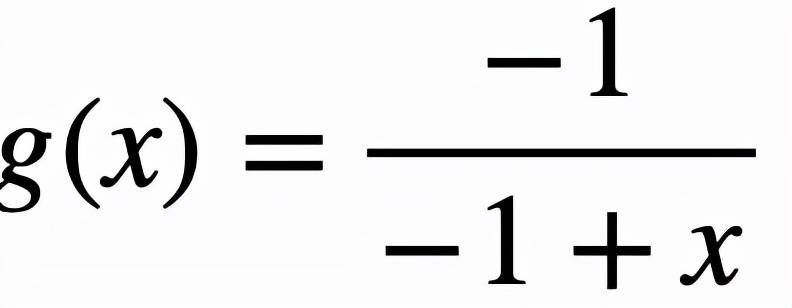
文章图片

， 这样对逻辑激活函数的改进可以
总结为

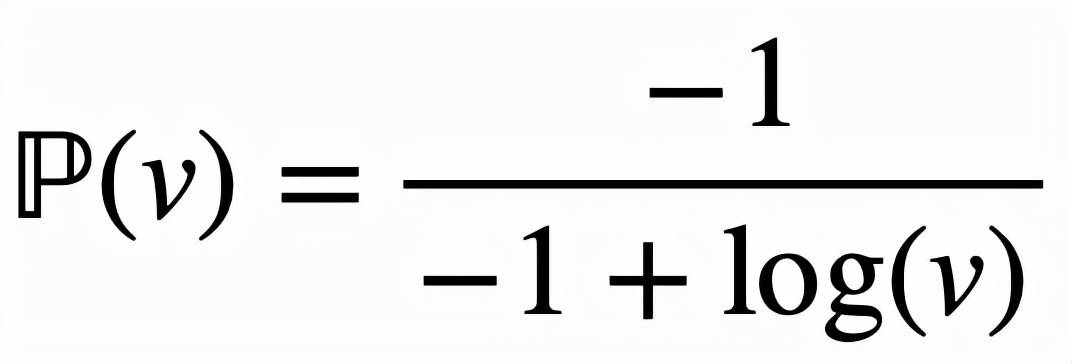
文章图片

， 而改进后的逻辑激活函数为：

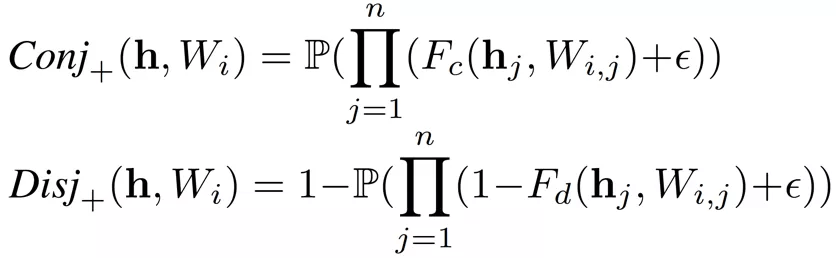
文章图片

二值化层
二值化层主要用于将连续的特征值划分为若干个单元 。 对于第 j 个连续值特征

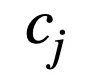
文章图片

， 有 k 个随机下界

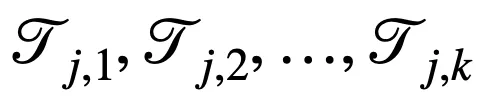
文章图片

和 k 个随机上界

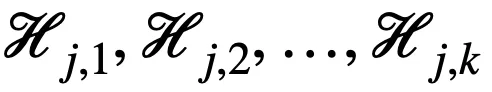
文章图片

对其进行划分 ， 进而得到以下二值向量
， 其中

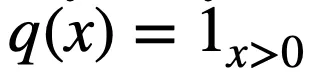
文章图片


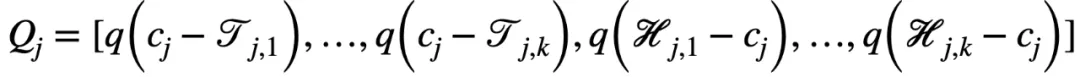
文章图片

由于逻辑层的边的连接是可以学习的 ， 因此通过组合一个二值化层和一个逻辑层 ， 模型可以实现自动选择适当的边界进行特征离散化（二值化） ， 即以端到端的方式对特征进行二值化 。 例如：