• 当一个合取层节点连接了和 ， 其表示区间
• 当一个析取层节点连接了和 ， 其表示区间

梯度嫁接法
虽然连续值版本的逻辑层能够使得整个 RRL 可导 ， 但是在连续空间内搜索一个离散值解仍是一个巨大的挑战 。 此外 ， 逻辑激活函数的特性导致 RRL 在离散点处的梯度几乎不含有用的信息 ， 因此像 Straight-Through Estimator (STE)这类方法无法训练 RRL 。
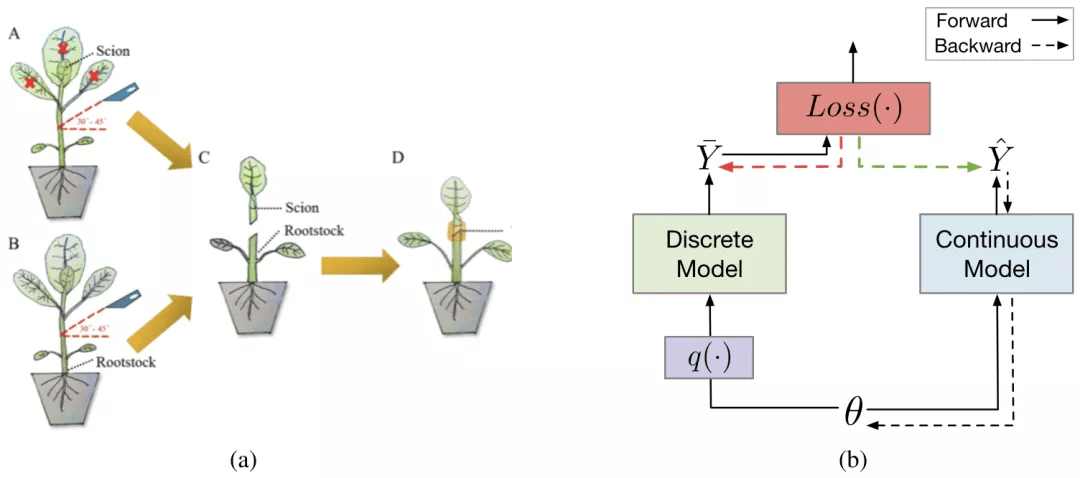
为了高效地对不可导的 RRL 进行训练 ， 论文提出了一种新的基于梯度的离散模型训练方法 ， 梯度嫁接法 。 在植物嫁接中（如图 3a 所示） ， 一种植物的枝或芽作为接穗 ， 而另一种植物的根或茎作为砧木 ， 嫁接到一起 ， 则得到了一种结合了二者优点的「新植物」 。 梯度嫁接法（Gradient Grafting）受植物嫁接方式的启发 ， 将损失函数对离散模型的输出的梯度作为接穗 ， 连续模型的输出对模型参数的梯度作为砧木 ， 进而构造出了一条完整的从损失函数到参数的反向传播路径（如图 3b 所示） 。 令

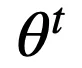
文章图片

为 t 时刻的参数 ，

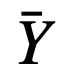
文章图片

和

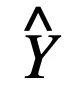
文章图片

分别为离散模型和连续模型的输出 ， 则：

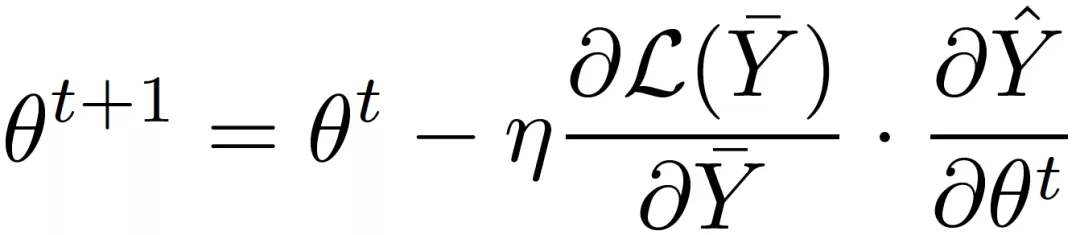
文章图片

梯度嫁接法同时使用了参数空间中连续点和离散点处的梯度信息 ， 并通过对两者的拆分组合 ， 实现了对离散模型的直接优化 。

文章图片

图 3：(a) 植物嫁接示例（Chen et al., 2019） 。 (b) 梯度嫁接法的简化计算图 。 实线和虚线箭头分别表示正向和反向传播 。 绿色箭头代表嫁接的梯度 ， 它是红色箭头代表的梯度的一个拷贝 。 嫁接后 ， 损失函数和参数之间存在一条反向传播路径 。
实验
论文通过实验来评估 RRL 并回答了如下问题：

1. RRL 的分类性能和模型复杂度如何？
2. 相较于其他离散模型训练方法 ， 梯度嫁接法收敛如何？
3. 改进后的逻辑激活函数的可扩展性如何？

作者在 9 个小规模数据集和 4 个大规模数据集上进行了实验 。 这些数据集被广泛用于测试模型的分类效果以及可解释性 。 表 1 总结了这 13 个数据集的基本信息 ， 可以看出 ， 这 13 个数据集充分体现了数据的多样性：实例数从 178 到 102944 ， 类别数从 2 到 26 ， 原始特征数从 4 到 4714 。 此外 ， 数据集的特征类型和稀疏程度也各有差异 。

文章图片

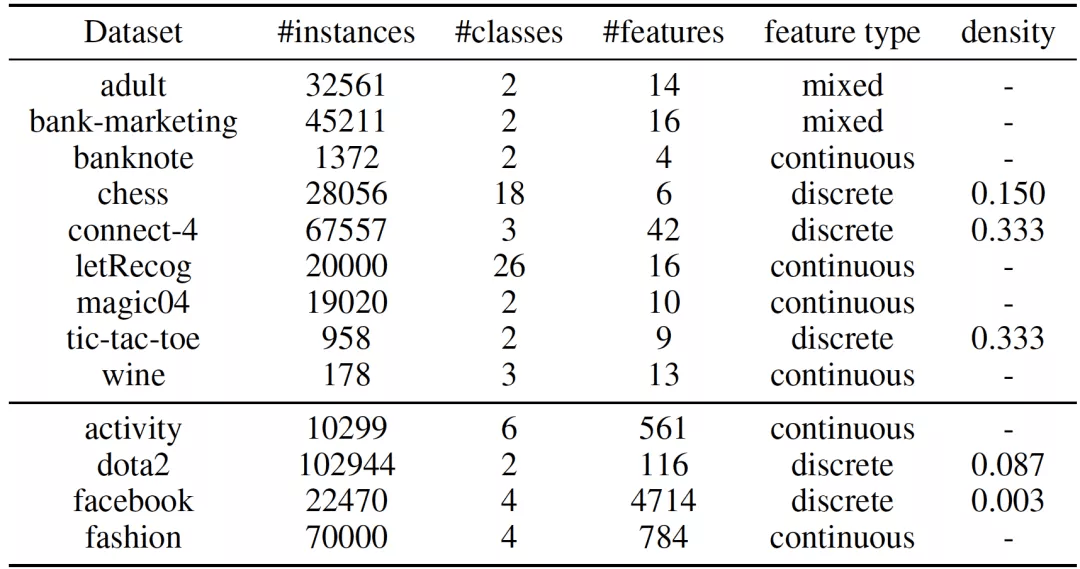
表 1：数据集统计信息
分类效果
论文将 RRL 的分类效果（F1 Score）与六个可解释模型以及五个复杂模型进行了对比 ， 结果如表 2 所示 。 其中 C4.5（Quinlan, 1993） ，CART（Breiman, 2017） ， Scalable Bayesian Rule Lists（SBRL）（Yang et al., 2017） ， Certifiably Optimal Rule Lists（CORELS）（Angelino et al., 2017）和 Concept Rule Sets（CRS）（Wang et al., 2020）是基于规则的模型 ， 而 Logistic Regression（LR）（Kleinbaum et al., 2002） 是一个线性模型 。 这六个模型被认为是可解释的 。 Piecewise Linear Neural Network（PLNN）（Chu et al., 2018） ，Support Vector Machines（SVM）（Scholkopf and Smola, 2001） ， Random Forest（Breiman, 2001） ， LightGBM（Ke et al., 2017）和 XGBoost（Chen and Guestrin, 2016）被认为是难以解释的复杂模型 。 PLNN 是一类使用分段线性激活函数的多层逻辑感知机（Multilayer Perceptron, MLP） 。 RF ， LightGBM 和 XGBoost 均为集成模型 。