模型：模型是基于 Battaglia 等人在 2018 年提出的交互网络（Interaction Network）的图神经网络 (GNN) 。 GNN 非常适合物理数据集：它们通过消息传递显式地处理对象（节点）之间的交互 ， 并允许研究者轻松地将对称（如置换、平移和旋转等）嵌入到网络中 。
GNN 的唯一输入是天体在给定时刻的位置和速度 ， 以及学习参数 。 通过训练 GNN 来预测每个天体的加速度 ， 模拟系统的动力学 ， 以及天体的质量 。

文章图片

蒸馏符号规则
接下来 ， 研究者希望找出 GNN 实际学会了哪些规则来预测这些动态 。 将模型压缩为一组符号规则也可以提高泛化能力 。
为此 ， 该研究使用符号回归拟合 GNN 消息传递模块的输入和输出 。 符号回归是一种机器学习算法 ， 可搜索数百万个符号表达式以拟合数据 。 该研究使用 PySR 算法 (Cranmer, 2022) 来完成这项任务 ， 其中用到了一种进化算法 。
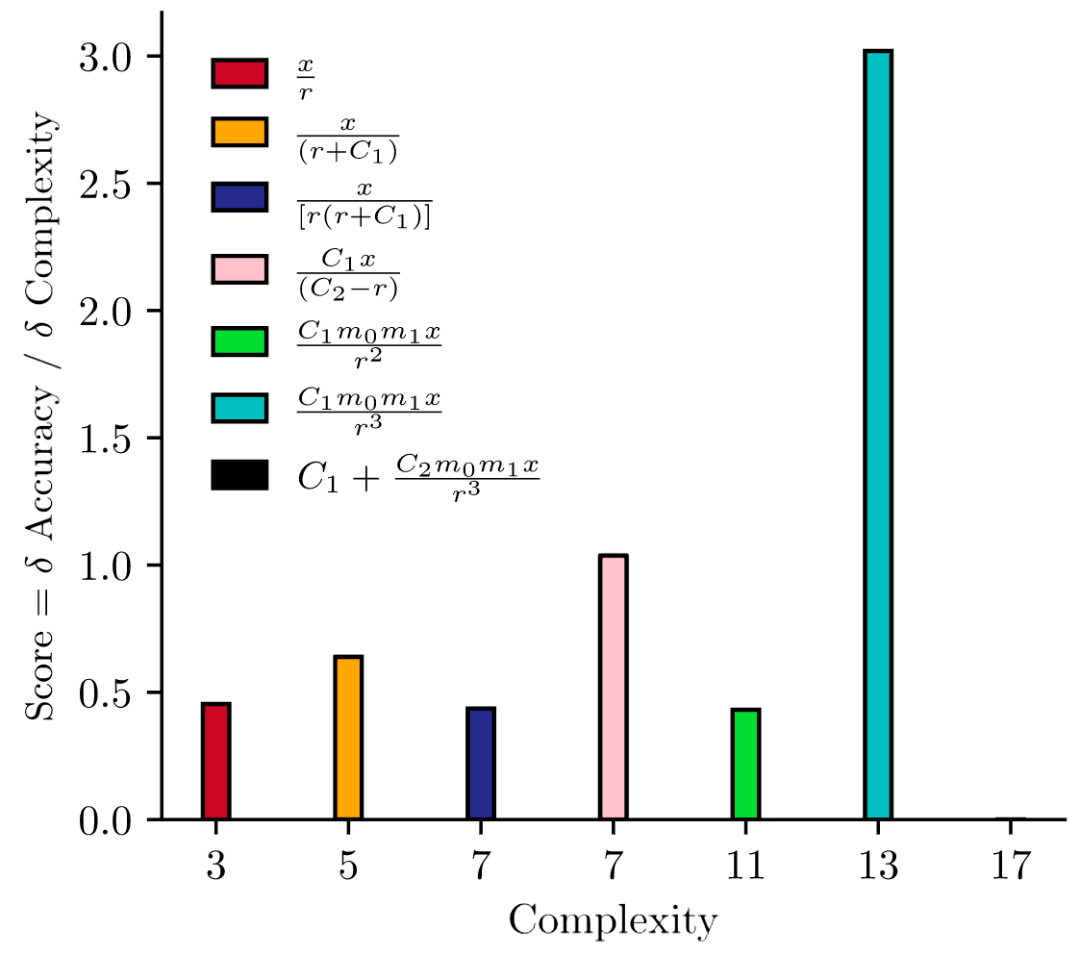
下图是从已经过学习的模拟器中发现的符号表达式 ， 从中可以发现所有情况下输出变量都是 F_x ，

文章图片

更复杂的表达式能更准确地逼近 GNN 的内部函数 。 然而 ， 人们总是可以在一个简单的表达式中添加其他项来提高它的准确性 ， 所以简单性和准确性是可以权衡的 。 该研究使用与 Cranmer 等人 (2020) 相同的分数 ， 成功地模拟了牛顿的万有引力定律（如上图蓝绿色所示） 。
然后研究者把这个已模拟的规律 ， 放回 GNN 的消息传递模块中 ， 得到的模拟效果如下：

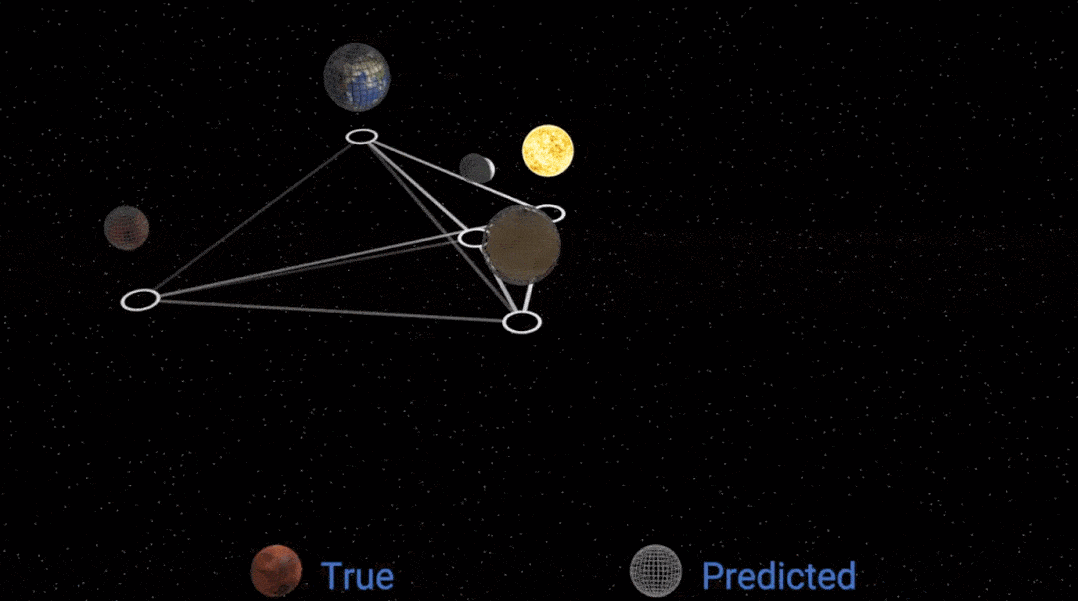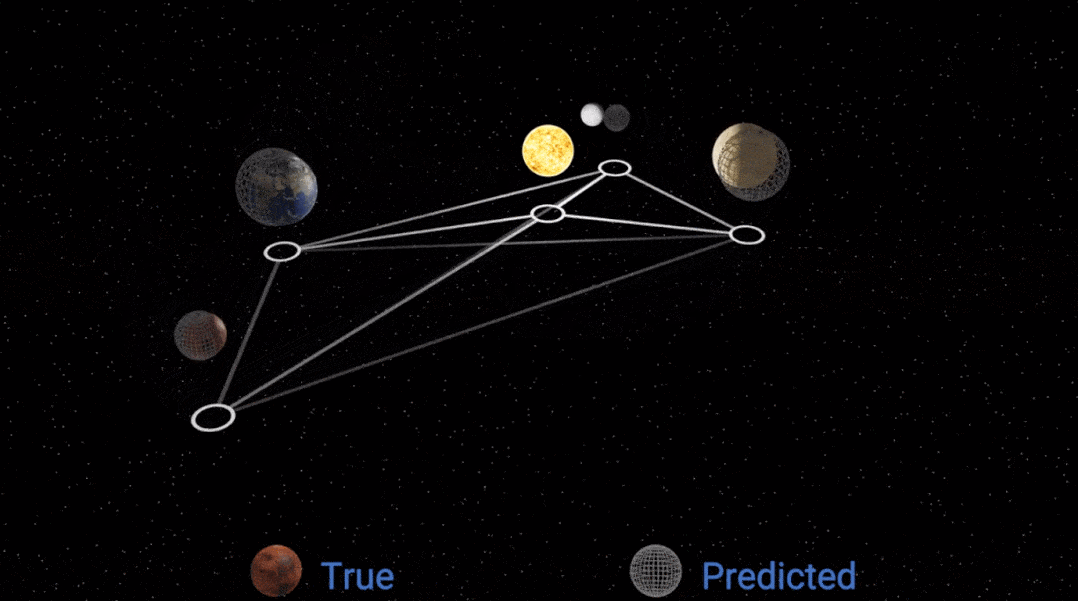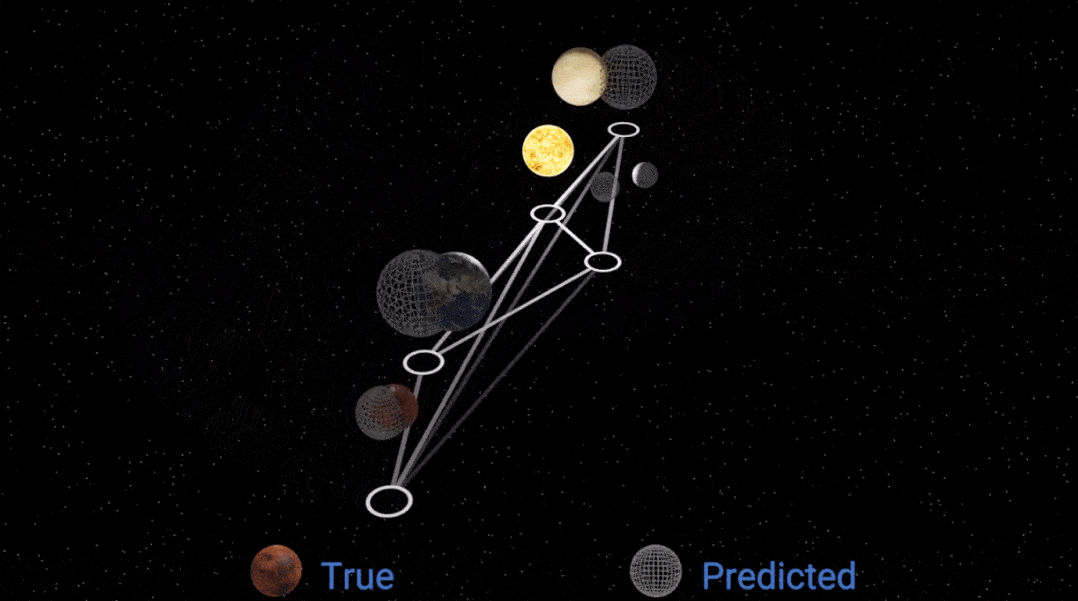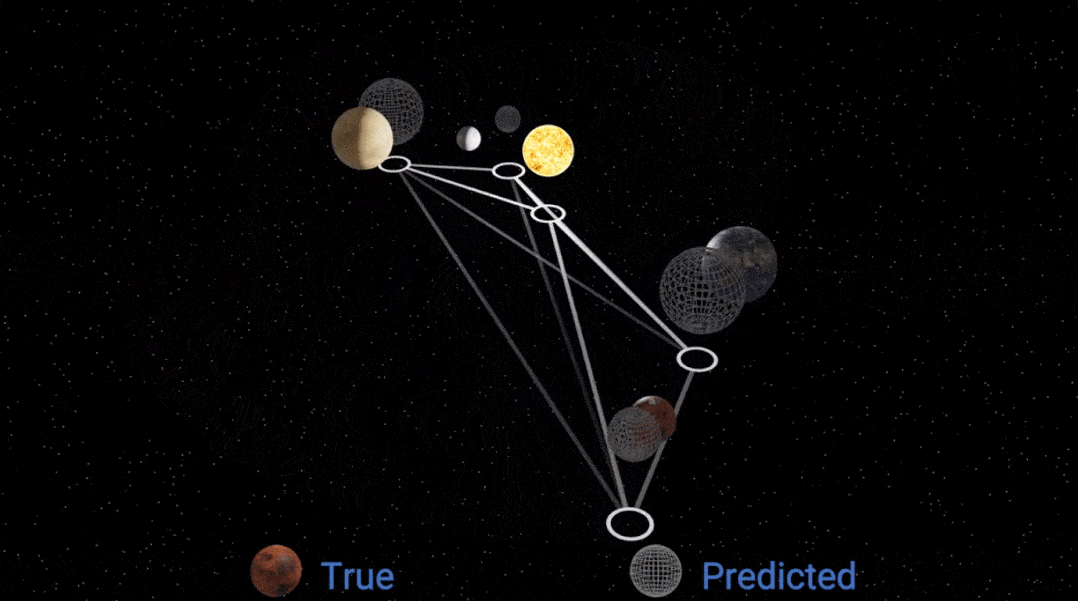
文章图片

显然 ， 性能变好了一些 ， 但仍然不完美 ， 为什么？
为了解决这个问题 ， 研究者首先比较了每个天体的算法估计质量与真实质量（归一化到太阳的质量范围内）：

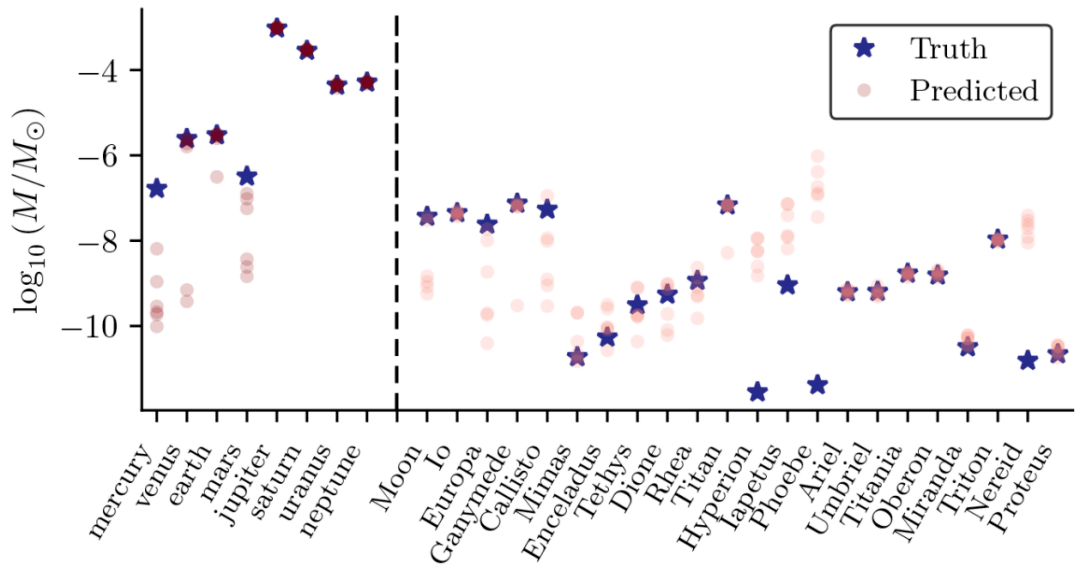
文章图片

与每个天体的真实质量相比 ， 模型估计的质量偏差很大 ， 有时甚至相差几个数量级 。
虽然 GNN 中的消息传递函数能够很好地近似牛顿万有引力定律 ， 但并不能完全精准地拟合 。 神经网络可以高度学习非线性函数 ， 但这些质量参数可能对 GNN 来说是良好输入 ， 却不是 GNN 符号版本的最佳输入 。
因此 ， 该研究决定通过固定的符号表达式重新拟合质量参数 ， 这种改进确实产生了更好的效果：

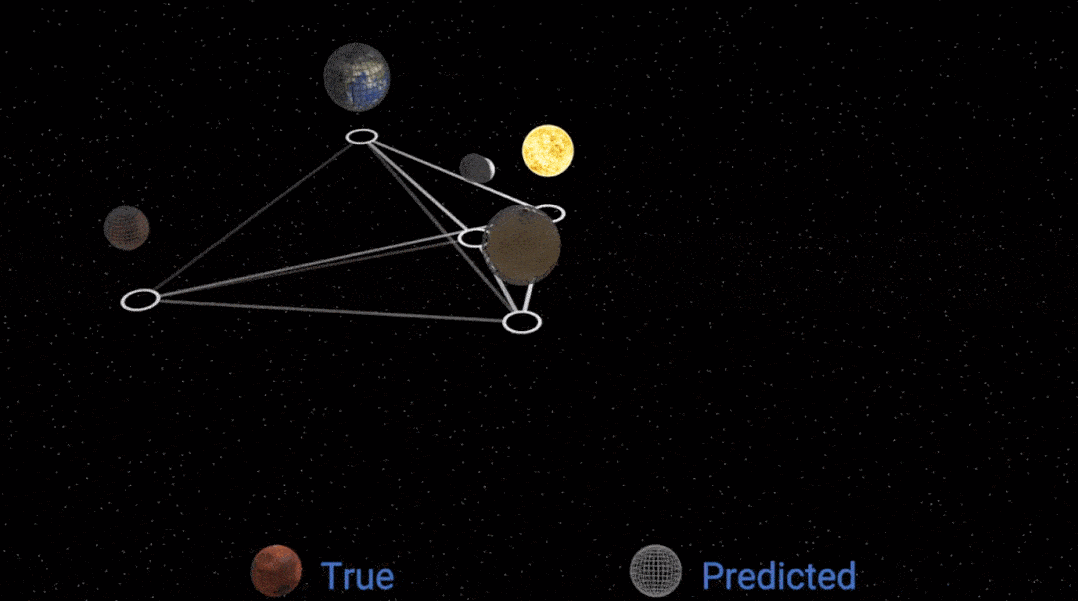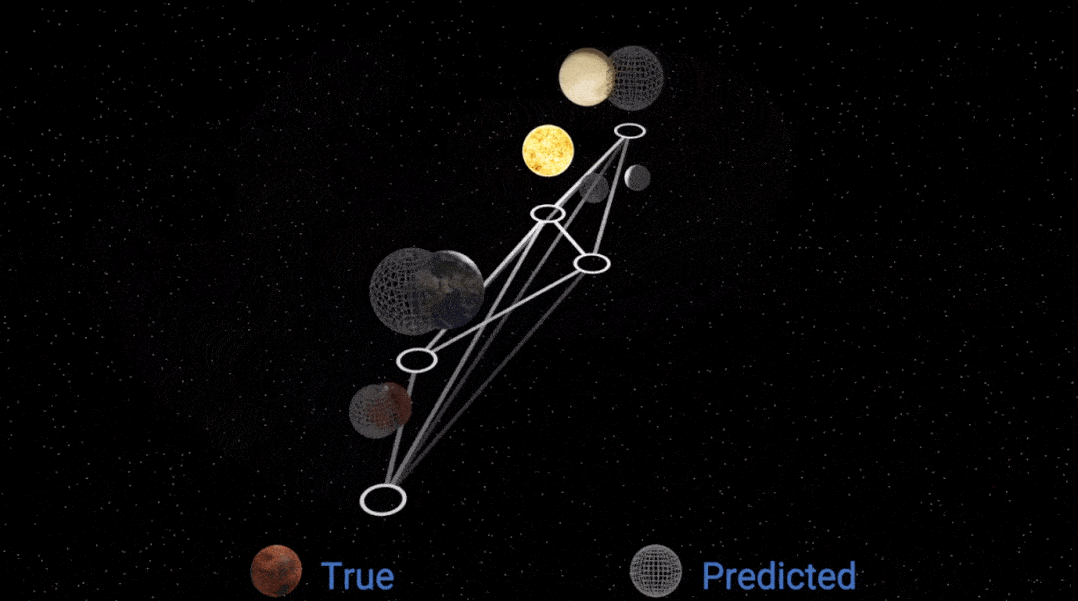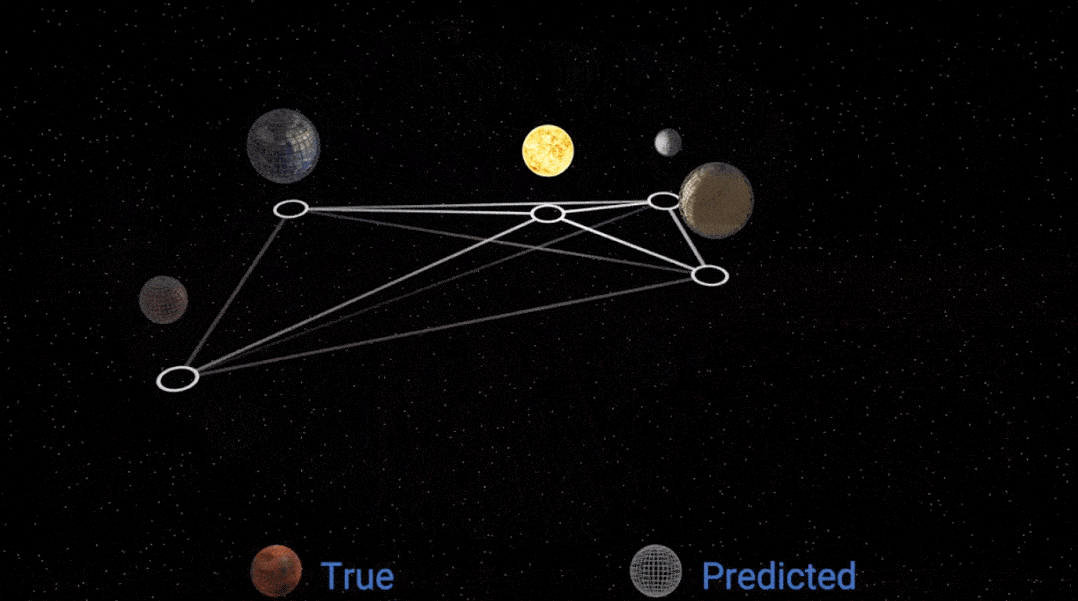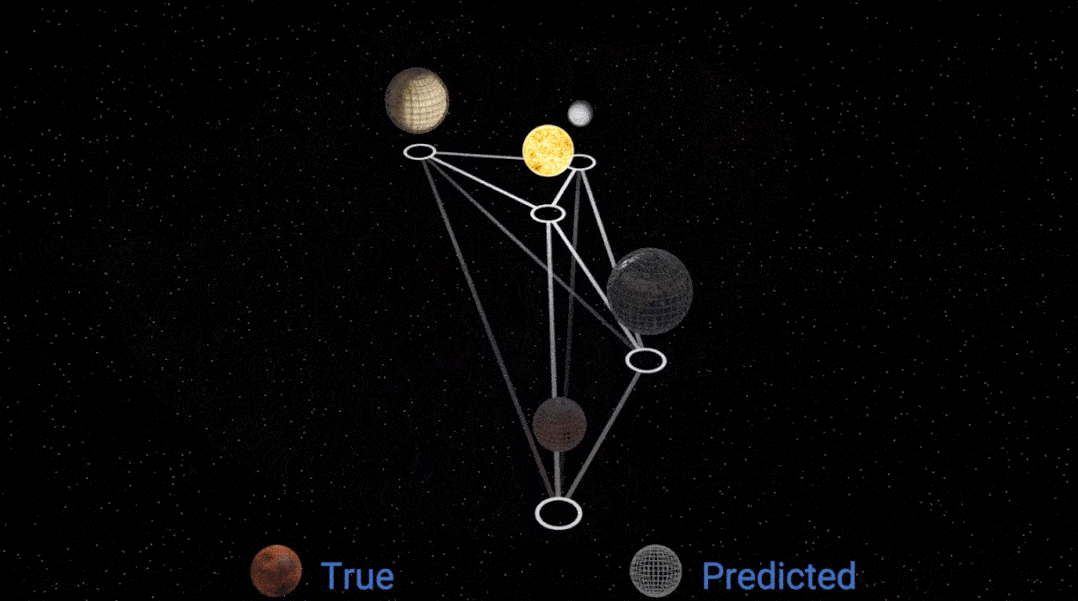
文章图片

此时 ， 模型重新估计的天体质量和真实质量的比较结果如下图所示：

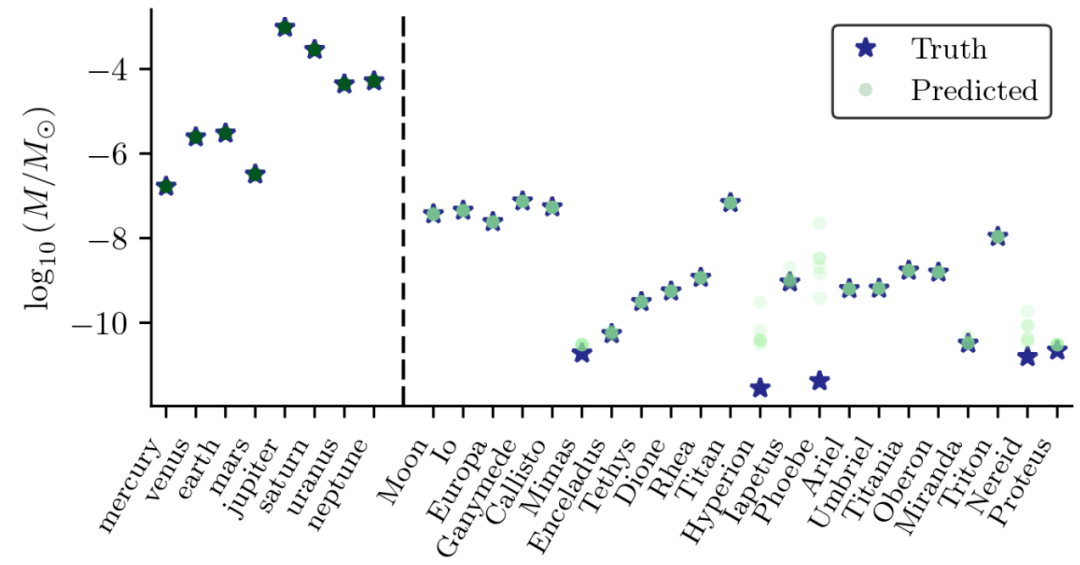
文章图片

改进之后 ， 模型估计的天体质量几乎完全匹配真实质量 。 为了解释这一点 ， 研究者认为需要做的是证明该算法的有效性 。
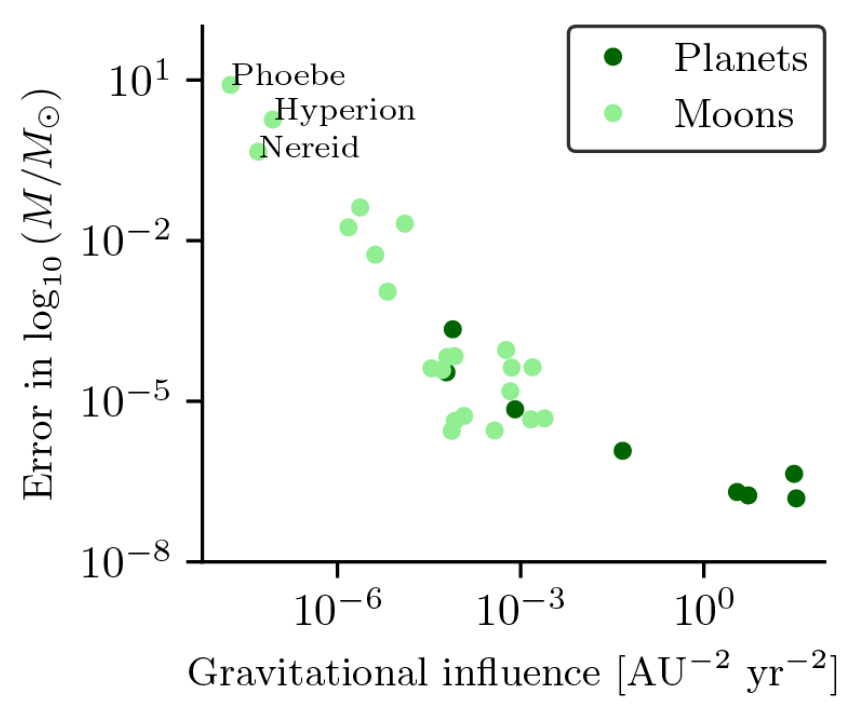
我们知道 ， 天体的质量只影响它对其他天体的引力 ， 例如如果地球变成两倍大 ， 月球轨道会受到很大影响 ， 但地球环绕太阳的轨道会保持不变 。 对于像 Phoebe、Hyperion 和 Nereid 这样的天体 ， 由于它们是非常小的卫星 ， 对其他天体轨迹的影响可以忽略不计 。 因此 ， 只要它们的质量很小就不会以任何方式影响系统 。 为了证实这一理论 ， 研究者估计了每个天体对其他天体的引力影响 ， 并联合质量估计的误差作图 。