机器之心报道
编辑：小舟、陈萍

如果牛顿没被苹果砸中 ， GNN 和符号回归也能发现万有引力定律？

机器学习 (ML) 推动了科学的巨大进步 ， 从粒子物理学到结构生物学再到宇宙学 ， 机器学习能够在大型数据集中学习特征 ， 对不同的对象进行分类 ， 并执行参数推断 ， 以及更具开创性的应用 ， 例如自回归语言模型、预测蛋白质结构 ， 以及蛋白质功能预测 。
机器学习强大的学习能力 ， 我们不禁会问 ， 机器学习能否仅仅通过观察我们的太阳系来重新发现万有引力定律？
牛顿的万有引力定律指出 ， 两个质点彼此之间相互吸引的作用力 ， 是与它们的质量乘积成正比 ， 并与它们之间的距离成平方反比 。 它是经典力学的一部分 ， 是在 1687 年于《自然哲学的数学原理》中首次发表的 ， 并于 1687 年 7 月 5 日首次出版 。

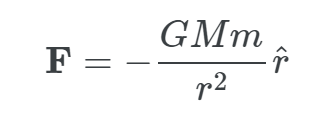
文章图片

近日来自萨塞克斯大学、伦敦大学学院等机构的研究者在论文《 Rediscovering orbital mechanics with machine learning 》中对上述问题进行的解答 ， 他们的回答是：可以 。

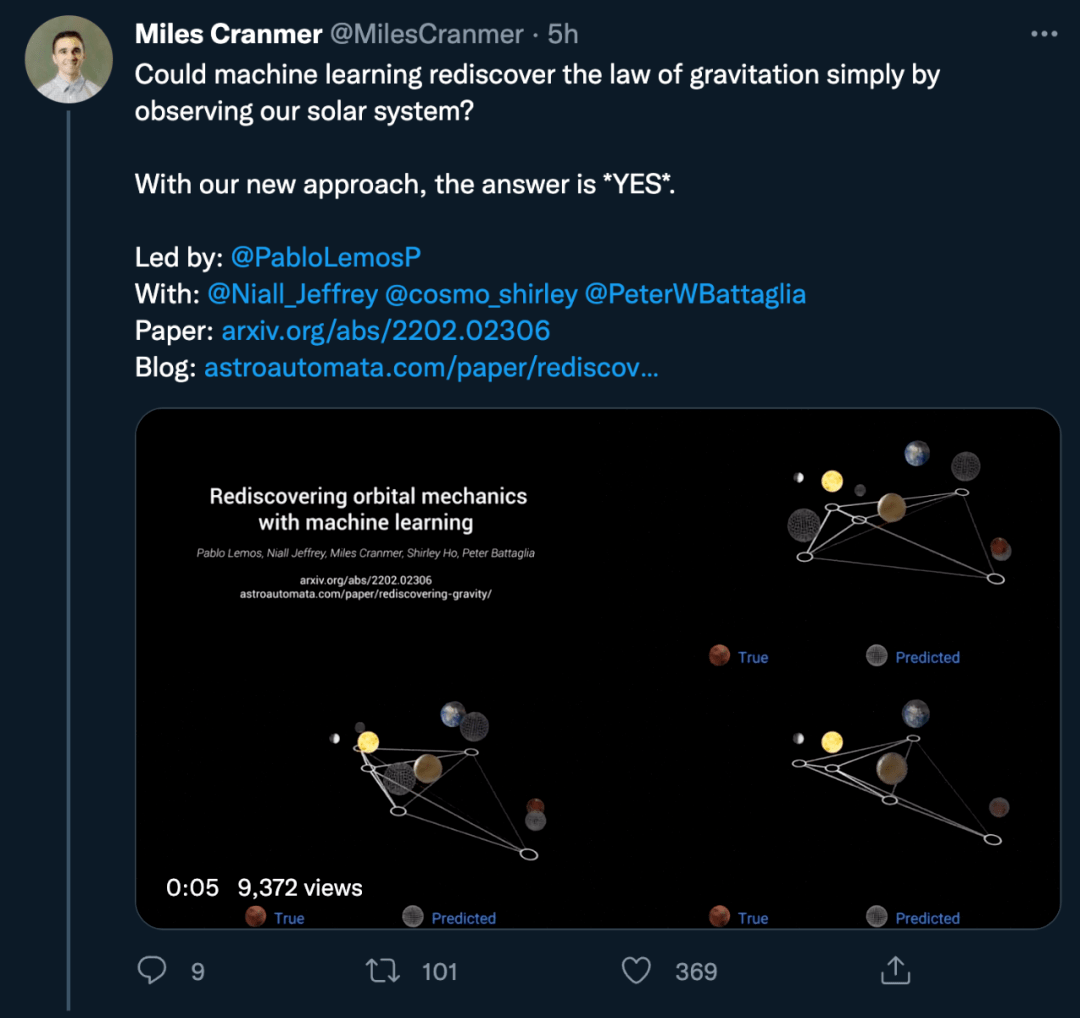
文章图片

论文作者之一 Miles Cranmer 推特截图
具体而言 ， 该研究提出了一种采用机器学习方法 ， 通过观察自动发现实际物理系统的控制方程和隐藏属性 。 研究者训练了一个图神经网络 ， 通过 30 年的轨迹数据来模拟太阳系的太阳、行星和大型卫星的动力学 。 然后 ， 他们使用符号回归来发现神经网络隐式学习的力学定律解析表达式 ， 结果表明表达式等效于牛顿万有引力定律 。

文章图片

论文地址：https://arxiv.org/pdf/2202.02306.pdf
该研究分为两个阶段：第一阶段的学习模拟器基于图网络 (GN) ， 图网络是一种深度神经网络 ， 可以通过训练来逼近图上的复杂函数 。 在这里 ， 太阳系的太阳、行星和卫星的（相对）位置和速度被表示为输入图的节点 ， 而天体之间可能的物理交互（例如力）被表示为图的边 。 该研究将基于 GN 的模拟器与 30 年来观测到的太阳系轨迹进行了拟合 。
在第二阶段 ， 该研究分离边函数（edge function） ， 并应用符号回归拟合边函数的解析公式 ， 其最好的拟合是对牛顿万有引力定律的拟合 。 然后 ， 该研究使用已发现的方程重新拟合未观察到的（相对）天体质量 ， 并找到了与天体真实质量几乎完美的拟合 。 之后研究者可以使用发现的方程和重新学习的质量来模拟太阳系动力学 ， 并获得与真实观察到的轨迹非常接近的对应关系 。
下图为太阳、水星、金星、地球和火星的示意图 ， 以及学习模拟器使用的相应图结构 。 图的节点代表天体 ， 边的亮度与它们之间的引力相互作用的强度成正比 。

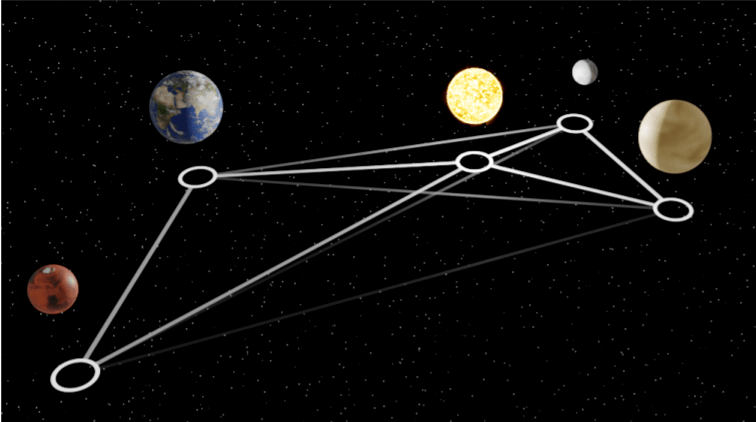
文章图片

数据与模型
数据：符号回归研究历来都专注于玩具（toy）模拟 ， 但是现实世界的数据充满了混乱 ， 包括噪音、信息丢失、未知的物理常数等 。 因此该研究直接从对太阳系的观察中重新发现轨道力学 。
该研究基于 NASA Horizons 的星历表 （Ephemeris）数据开发了一个训练数据集 ， 数据集包括太阳系中质量超过 10^18 kg 的 31 个天体：太阳、行星、冥王星和一系列卫星 。 训练数据来自 1980 年到 2010 年的 30 年期间的数据 ， 验证集来自 2010-2013 年的数据 。