文章图片




文章图片




文章图片




文章图片




文章图片




女士们 ， 先生们 ， 老少爷们儿们！在下张大少 。
长期以来 ， 设计师和艺术家对覆盖表面的马赛克感兴趣 。 然而最近 ， 数学家们将注意力转向了这种视觉呈现 ， 并发现它们是有趣的问题的迷人来源 ， 其中许多问题仍未解决 。
荷兰艺术家埃舍尔 (1898-1972)经常将平面的规则分割描述为“我所获得的最丰富的灵感来源”[1
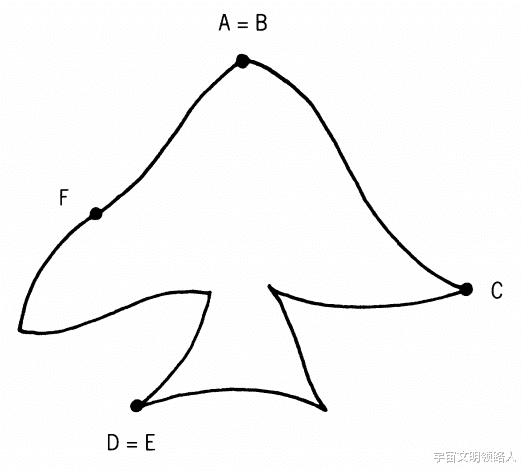
。 在马约利卡瓷砖、镶嵌木材、砌砖、雕刻灰泥、石头路面、缝制拼布或印花织物中展示的联锁形状对许多人来说具有特殊的魅力 ， 远远超过这些图案提供的美感 。 镶嵌可以作为一个范例：它完全是视觉化的(也许看起来纯粹是设计的起源) ， 但作为数学问题的来源 ， 它却异常丰富 。 这些问题对那些(像埃舍尔一样)设计复杂而不寻常的镶嵌工艺的人来说 ， 都有一定的意义 。 其他问题探索镶嵌的可能性的限制 ， 研究镶嵌的结构 ， 旨在产生分类的方法或将镶嵌与自然的物理结构或虚拟的数学结构联系起来 。
数学家试图了解瓷砖如何铺砌表面——不仅是欧几里得平面 ， 还包括双曲平面和三维物体的表面 ， 如球体、圆环(甜甜圈)或莫比乌斯带[2
。 他们还研究在我们的三维世界中不可能完全表示的表面上的瓷砖 ， 比如克莱因瓶或更高维度的表面 。 瓷砖的问题不仅仅局限于表面——还有很多奇妙的问题 ， 比如三维的“瓷砖”(如多面体)如何填充空间 ， 或者更高维度的空间如何填充瓷砖 。
这些问题大部分都很难 ， 而且大部分都没有解决 ， 但是人们正在努力解决 。 如果我们把自己限制在关于给欧几里得平面密铺的问题上 ， 这个主题仍然是非常丰富的 ， 而且还远远没有完成 。 在这篇文章中 ， 我将强调一些不同种类的数学问题 ， 这些问题可能与欧几里得平面的密铺有关 。 有些问题得到了充分的回答 ， 有些问题只得到部分回答 ， 有些问题根本没有得到回答 。 尽管数学家和科学家已经研究了这些问题(现在仍然如此) ， 但许多问题对于那些很少或没有受过正式数学训练的人来说是容易理解的 。 尝试各种可能性可以带来很多乐趣 ， 甚至可能导致重大发现 。
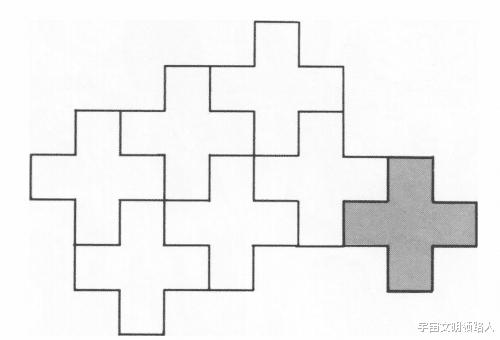
密铺是平面上没有间隙或重叠的闭合形状的覆盖；另外两个同义术语是镶嵌和拼花 。 当然 ， 真正的瓷砖在相邻的瓷砖之间有一个很小的空间 ， 里面填满了水泥、胶水或者只是普通的泥土；从数学上来说 ， 这个空间被视为瓷砖的厚重轮廓 ， 它们(至少在理论上)完美地组合在一起 。 将各种形状组合起来填充一个区域是一项令人愉快的挑战——玩彩色多边形或完成拼图游戏都是给出形状的例子 ， 我们希望它们至少以一种方式组合在一起 。 众所周知 ， 为儿童探索镶嵌而制作的简单多边形可以以许多不同的方式组合在一起；拼图玩具的形状肯定能拼在一起 ， 因为它们同时被一个模具切割 ， 模具的切割边缘勾勒出一个与完成的拼图大小相等的矩形 。